6. Example 6: Three-bar Truss Design

Example of solving the constrained engineering optimization problem “Three-bar truss design” using NEORL with the BAT, GWO, and MFO algorithms.

6.1. Summary

  • Algorithms: BAT, GWO, MFO

  • Type: Continuous, Single-objective, Constrained

  • Field: Structural Engineering

6.2. Problem Description

The Three-bar truss design is an engineering optimization problem with the objective to evaluate the optimal cross sectional areas \(A_1 = A_3 = x_1\) and \(A_2 = x_2\) such that the volume of the statically loaded truss structure is minimized accounting for stress \((\sigma)\) constraints. The figure below shows the dimensions of the three-bar truss structure.

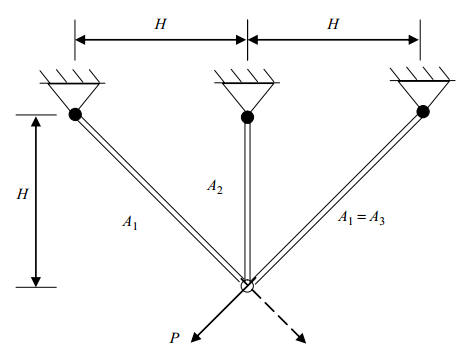
alternate text

The equation for the volume of the truss structure is

\[\min_{\vec{x}} f (\vec{x}) = (2 \sqrt{2} x_1 + x_2) \times H,\]

subject to 3 constraints

\[ \begin{align}\begin{aligned}g_1 = \frac{\sqrt{2} x_1 + x_2}{\sqrt{2} x_1^2 + 2 x_1 x_2} P - \sigma \leq 0,\\g_2 = \frac{x_2}{\sqrt{2} x_1^2 + 2 x_1 x_2} P - \sigma \leq 0,\\g_3 = \frac{1}{x_1 + \sqrt{2} x_2} P - \sigma \leq 0,\end{aligned}\end{align} \]

where \(0 \leq x_1 \leq 1\), \(0 \leq x_2 \leq 1\), \(H = 100 cm\), \(P = 2 KN/cm^2\), and \(\sigma = 2 KN/cm^2\).

6.3. NEORL script

#---------------------------------
# Import packages
#---------------------------------
import numpy as np
from math import cos, pi, exp, e, sqrt
import matplotlib.pyplot as plt
from neorl import BAT, GWO, MFO

#---------------------------------
# Fitness function
#---------------------------------
def TBT(individual):
    """Three-bar truss Design
    """
    x1 = individual[0]
    x2 = individual[1]
    
    y = (2*sqrt(2)*x1 + x2) * 100
    
    #Constraints
    if x1 <= 0:
    	g = [1,1,1]
    else:
    	g1 = (sqrt(2)*x1+x2)/(sqrt(2)*x1**2 + 2*x1*x2) * 2 - 2
    	g2 = x2/(sqrt(2)*x1**2 + 2*x1*x2) * 2 - 2
    	g3 = 1/(x1 + sqrt(2)*x2) * 2 - 2
    	g = [g1,g2,g3]
    
    g_round=np.round(np.array(g),6)
    w1=100
    w2=100
    
    phi=sum(max(item,0) for item in g_round)
    viol=sum(float(num) > 0 for num in g_round)
    
    return y + w1*phi + w2*viol
#---------------------------------
# Parameter space
#---------------------------------
nx = 2
BOUNDS = {}
for i in range(1, nx+1):
    BOUNDS['x'+str(i)]=['float', 0, 1]


#---------------------------------
# BAT
#---------------------------------
bat=BAT(mode='min', bounds=BOUNDS, fit=TBT, nbats=10, fmin = 0 , fmax = 1, A=0.5, r0=0.5, levy = True, seed = 1, ncores=1)
bat_x, bat_y, bat_hist=bat.evolute(ngen=100, verbose=1)

#---------------------------------
# GWO
#---------------------------------
gwo=GWO(mode='min', fit=TBT, bounds=BOUNDS, nwolves=10, ncores=1, seed=1)
gwo_x, gwo_y, gwo_hist=gwo.evolute(ngen=100, verbose=1)

#---------------------------------
# MFO
#---------------------------------
mfo=MFO(mode='min', bounds=BOUNDS, fit=TBT, nmoths=10, b = 0.2, ncores=1, seed=1)
mfo_x, mfo_y, mfo_hist=mfo.evolute(ngen=100, verbose=1)

#---------------------------------
# Plot
#---------------------------------
plt.figure()
plt.plot(bat_hist['global_fitness'], label = 'BAT')
plt.plot(gwo_hist['fitness'], label = 'GWO')
plt.plot(mfo_hist['global_fitness'], label = 'MFO')
plt.legend()
plt.xlabel('Generation')
plt.ylabel('Fitness')
plt.savefig('TBT_fitness.png',format='png', dpi=300, bbox_inches="tight")
plt.show()

6.4. Results

A summary of the results for the three differents methods is shown below with the best \((x_1, x_2)\) and \(y=f(x)\) (minimum volume).

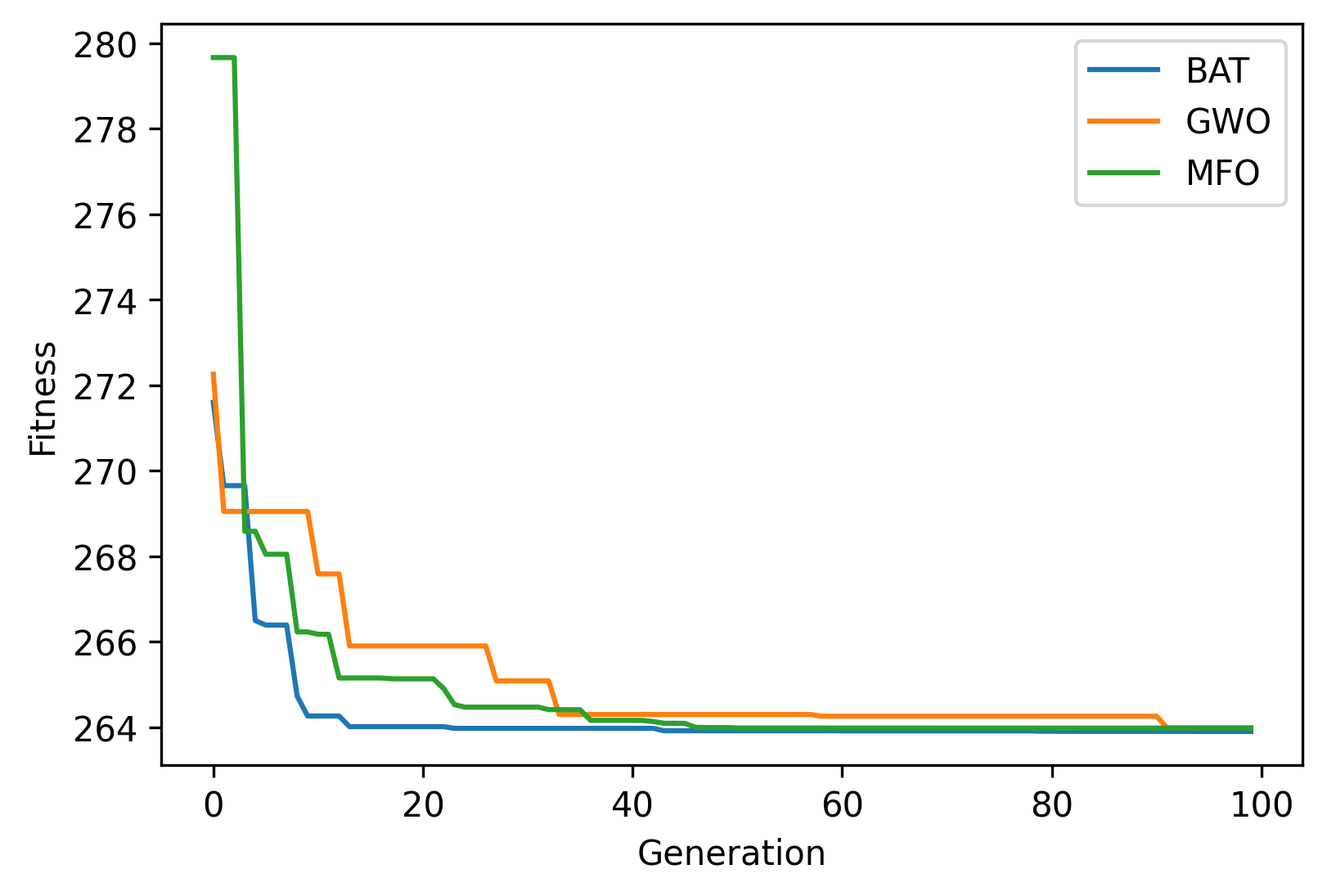
alternate text 
------------------------ BAT Summary --------------------------
Best fitness (y) found: 263.90446934840577
Best individual (x) found: [0.79190302 0.39920471]
--------------------------------------------------------------
------------------------ GWO Summary --------------------------
Best fitness (y) found: 263.99180199625886
Best individual (x) found: [0.78831222 0.41023435]
--------------------------------------------------------------
------------------------ MFO Summary --------------------------
Best fitness (y) found: 263.9847325242824
Best individual (x) found: [0.77788022 0.4396698 ]
--------------------------------------------------------------